When I first started college, I went to a lot of orientation-type events for math majors. Almost inevitably, somebody would pose a math puzzle to anybody who would listen. There’s one question that I still remember though, and I don’t even know who asked it; I just found it sketched in the corner of a blackboard with no solution or attribution (recreation shown below).
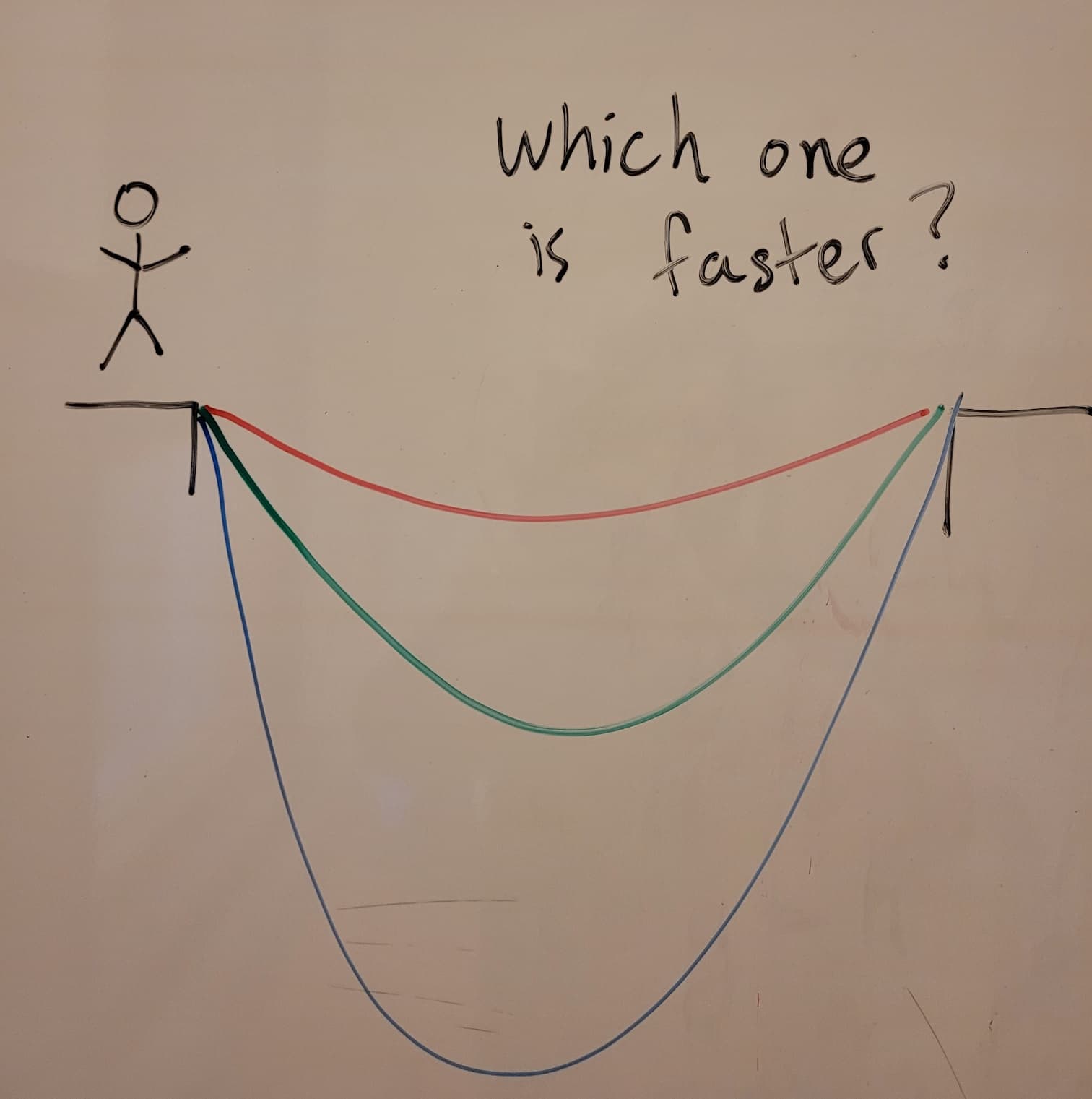
There isn’t a lot of detail to go on, but we can fill in the blanks ourselves. If you want to zipline as quickly as possible across a canyon of some fixed width, how much rope should you use? Intuitively, some finite length of rope must be optimal. If the rope is too short, you’ll accelerate really slowly at first; if the rope is too long, you’ll spend too much time in near free-fall before the rope catches you and pushes you towards the other side.
There are a lot of factors here to ignore; friction, drag, and perhaps most notably, the deformation of the rope itself as you slide across. If we assume that our mass is negligible compared to the rope, we can model the rope as a catenary defined by an equation like \(y = a\cosh(\frac{x}{a})\). With all this setup, it feels like there might be a chance of getting a nice answer with a bit of calculus. Unfortunately, I still haven’t been able to get a pretty answer; only some rough approximations with Mathematica. The formulas end up having a lot of radicals and, combined with the hyperbolic trig functions, they don’t turn into the easiest integrals.
My current best answer is that the rope should be roughly 31% longer than the canyon that you’re trying to cross, but there’s always the chance that I messed up somewhere! You can see my work here on Math.StackExchange if you’re curious about it.