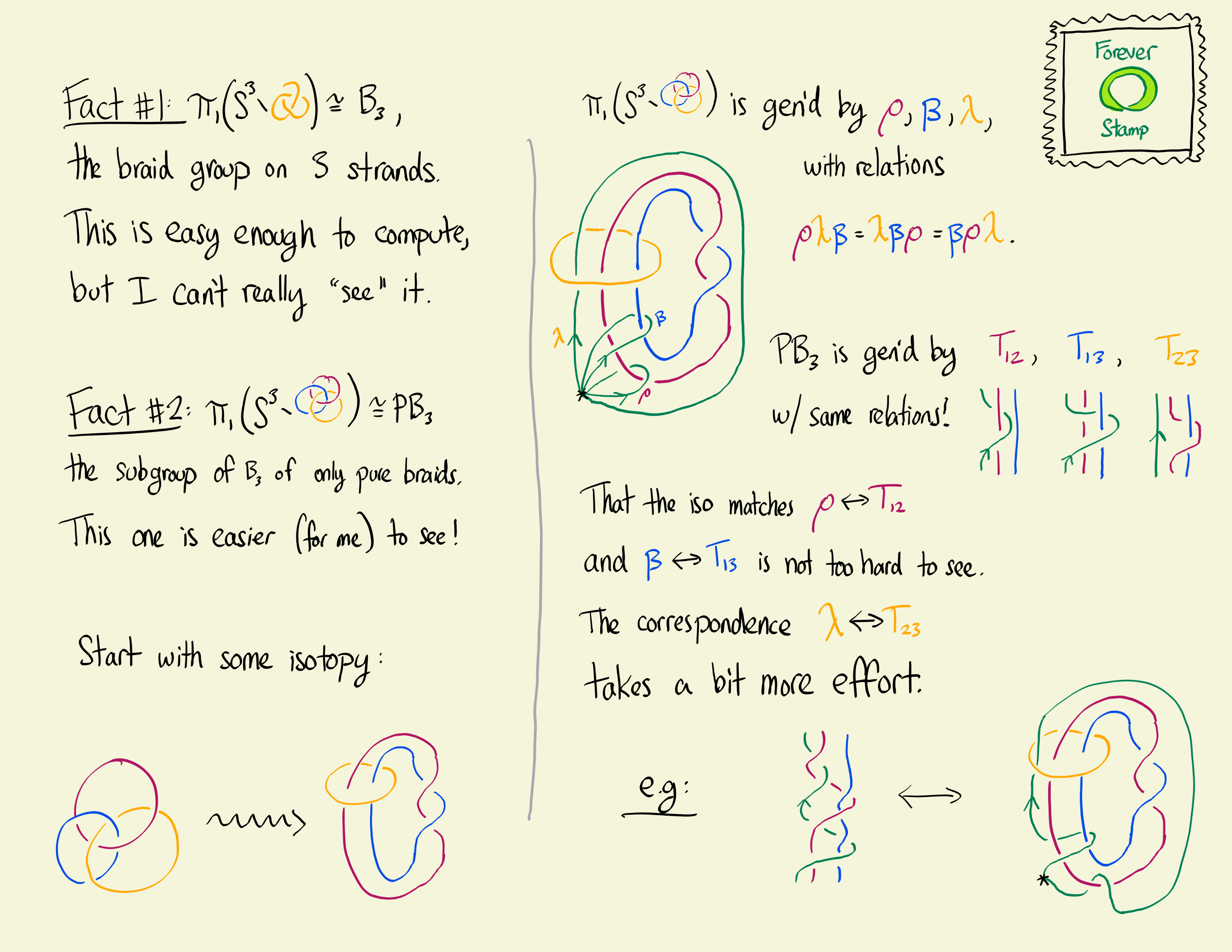This post was inspired by the postcard I submitted to NCNGT 2023 this year. It starts with the observation that \(\pi_1(S^3 \setminus T) \cong B_3\), where \(T\) is the trefoil knot and \(B_3\) is the 3-braid group. This is a pretty surprising fact, at least to me! The braid groups \(B_n\) only show up as link groups for \(n \le 3\) (see this StackExchange post), and the \(n=1,2\) cases aren’t that interesting (they correspond to the empty link and the unknot, respectively). As far as I can tell, this is mostly a coincidence, but I would love to be proven wrong (maybe one can find \(B_4\) in the complement of a knotted 2-sphere?).
Coincidence or not, though, there should be some way to visualize this isomorphism. Elements of a knot group look like pieces of string tied around a knot, and elements of a braid group look like multiple intertwined strings. One can compute the fundmadental group of the trefoil via the Wirtinger presentation, for example, but the generators that you end up with don’t look very much like 3-braids to me. Part of the issue is that \(\pi_1(S^3 \setminus T)\) is generated by loops starting and ending at a basepoint, whereas each braid strand may not end up in the same place that it started. This observation suggests that we might get a cleaner correspondence by looking at the pure braid group.
Interestingly enough, the pure 3-braid group \(PB_3\) also shows up as the complement of a link, which this time is the “3-component Hopf link” (see this StackExchange post). This is the isomorphism that actually ends up being easier for me to understand, visually. If you ignore one of the components of the link to get just a two component Hopf link, you can pretend that they are two of the three strands of a 3-braid. An element of \(\pi_1\) can be viewed as the third strand of our 3-braid, winding back and forth between the Hopf link components but eventually returning to where it started!
Anyway, here’s the postcard: